Topic018: T=7 Properties, Asymmetry’s Role, and Metallicity Relationships,
Bill Tifft 4/28/16

Book figure Appendix 2.19 upper and lower
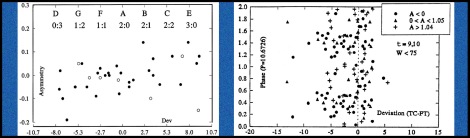
Book figures A2.20 and 3.49
T = 7 relates to extreme narrow profile irregular dwarfs, t = 9-10 with 21 cm profile widths less than 75 km/s. These objects cannot accommodate a 73 km/s nuclear dipole and have little if any of the two stream spiral character associated with such a nuclear structure or even have a clear nucleus. They appear to evolve rapidly in the T = 7 state, D (doubling) level 14 or 15 within a pattern of changing shape (asymmetry, A). The lower right frame of the lead figure in this topic (book figure 3.49) shows a phase-deviation diagram at the T = 7 10.6726 km/s period. (For book information or acquisition see Post001 and Post002.) At phase N.5, in negative form asymmetrically, the sharp upper edge could imply a brief stable pause below which several cascades may begin, pass through or near a positive asymmetry group and return to a negative form. The same may be possible beginning at the positive asymmetry group at phase N.0. However, if you sight back along the steep slopes near N.0 and N.5 the slopes do not intersect at the primary phase points. The figure maps a cycle of activity and change, not rapid change between stability which is the typical pattern seen. Phase-deviation patterns are optimal for effectively defining periods, not evolution cycles. Asymmetry associates with change, not stability. The slope offsets suggest a shift in the period might generate an actual `shape’ cycle in time. In fact such a period is already known. The short period 5.3313 was discussed in Topic009 (book figure 2.36) and is shown in the header figures for that Topic. That important period led to defining the cosmological correction, and generates the two top lead figures in this blog which now shows what is expected. Using a double phase cycle there are stable start points near or at symmetric profile groups and clear cascades, one showing positive asymmetry the other negative forms. Near symmetric forms are in both frames. Phase levels at 0.05 above N.0 and N.5 are marked with phase wrap letters which can define up to four parallel cascade lines, for example A – F – G – D (upper lines repeat, below the two marked, to track slope progression). The lower left leading figure shows there can be progression in asymmetry, although there could be two slopes splitting at A as a primary stable location . In quantum transitions changes in wave function overlap affects transition probabilities. Number pairs suggest the number of quantum steps, before or after passing zero deviation, to place points at a given spot. The pattern shows a consistent multi-slope rapid cascade between stable N.0 and N.5 points for an aggregate of objects, a good shape-deviation diagram.
The 5.3313 km/s period fits the data in Topic009 very well but is significantly different from 5.3363 km/s period (half of 10.6725 = 5.3363, both are c fractions). The difference can be explained, providing important confirmation of Quantum Temporal Cosmology (QTC). A slight quantum period adjustment, to match the `shape’ cycle, is actually required. In QTC there are two fundamental flow rates through time. Massless energy (photons) flows through time (laterally only, radial cosmic time does not pass for photons) at the `temporal’ speed of light, c(t). The doubling related radial steps of massless active energy photons (tabulated in book figure 3.7 as basic D,T fractions of c) are redshift `temporal’ radial decay quantum steps, not a flow. For space and matter, time (radial aging, the continuous flow of space) is slightly slower since special relativity applies. That slower rate of passage of time is what is used to define periods including our value of c(s). A slightly shorter period, with no lag, must define the temporal change-cycle period. This spatial – temporal shift is included in the cosmic – spatial rest frame transformation, defines the observed scale of the CBR dipole and the nature of dark matter in QTC (book chapter 7).
The discovery of the 5.3313 km/s shape-deviation period, and the detailed development of the clear cascade patterns at intermediate profile widths, occurred before the fractional c form of quantum redshift periods was found. Appendix 2, which was denied publication by the ApJ, contains a striking analysis of redshift variability (and commentary relating to the difficulty of publishing such information). In order for someone to continue such studies eventually, the unpublished data obtained on the 21 cm redshift standards at the Green Bank 140-foot telescope (with several other sets) is contained in Appendix 2. I will develop further aspects of timelines and galaxies in QTC in later Topics. Aspects of the redshift, asymmetry and alignment are very important. I will close this topic by presenting one further connection of T states to galaxy properties, namely metallicity in local dwarf and irregular systems. M. L. Mateo published a review in the 1998 Annual Review of Astronomy and Astrophysics (Vol 36, page 435) describing a puzzling difference in the metallicity properties between dwarf spheroidal and dwarf irregulars. Metal content is presumed to develop systematically over cosmic time and there is no apparent reason for two different patterns. Since detailed data including redshifts and morphological classifications was included, I checked for a T state distinction. The terminal figure in this Topic (book figure 3.28) shows that dwarf spheroidal forms are members of T = 6 (P = 5.7635) with no evidence for T = 0. The irregular classes are strongly periodic in T = 0 (P = 18.2979) with perhaps some spheroidal forms. Irregulars do not mix, but some forms of spheroidal may with a clear phase shift. I am quite sure that this distinction is a form of the T = 0/6 split in dwarf t forms discussed and illustrated in Topic015. Both the structural and astrophysical chemistry of galaxies is T dependent. I have little or no doubt that recognition rather than ignoring QTC could lead to major advances in understanding of galaxies and cosmology. At this point I will change the nature of the Topics to particle physics before returning to cosmology and still finer important details of what T states and galaxies are. Particles of matter in space are a lot like particles of space/matter in time.

Book figure 3.28
| ← Topic017 | Topic019 → |

